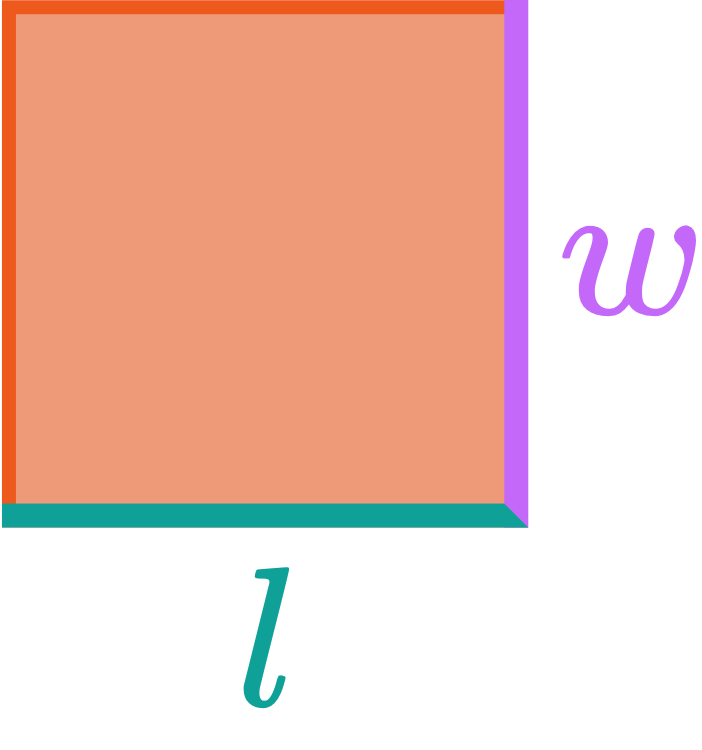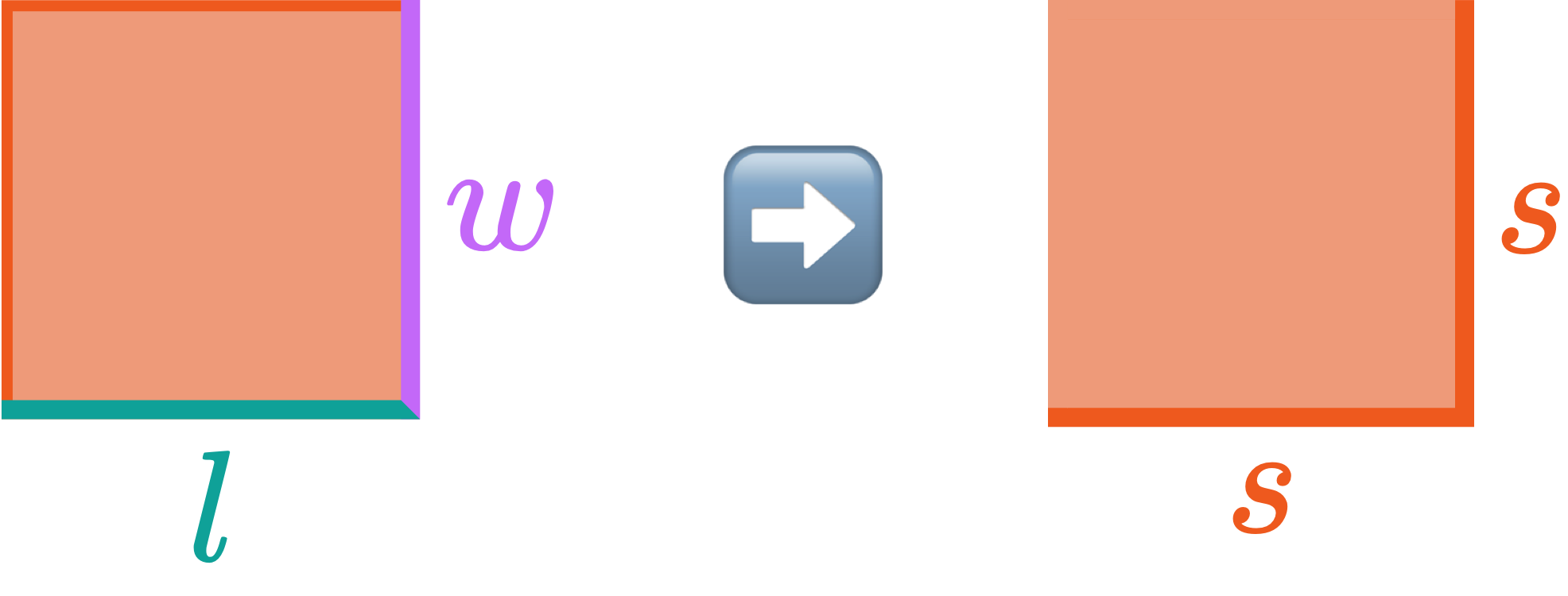QUICK LINKS

STUDENT
TEACHER

Area of Quadrilaterals Calculator

QUICK LINKS

STUDENT
TEACHER

Area of Quadrilaterals Calculator

Area of Quadrilaterals

CALCULATOR
—

Area of Quadrilaterals Calculator

What does your quadrilateral look like?

Step 1. Identify the length & width of the rectangle.

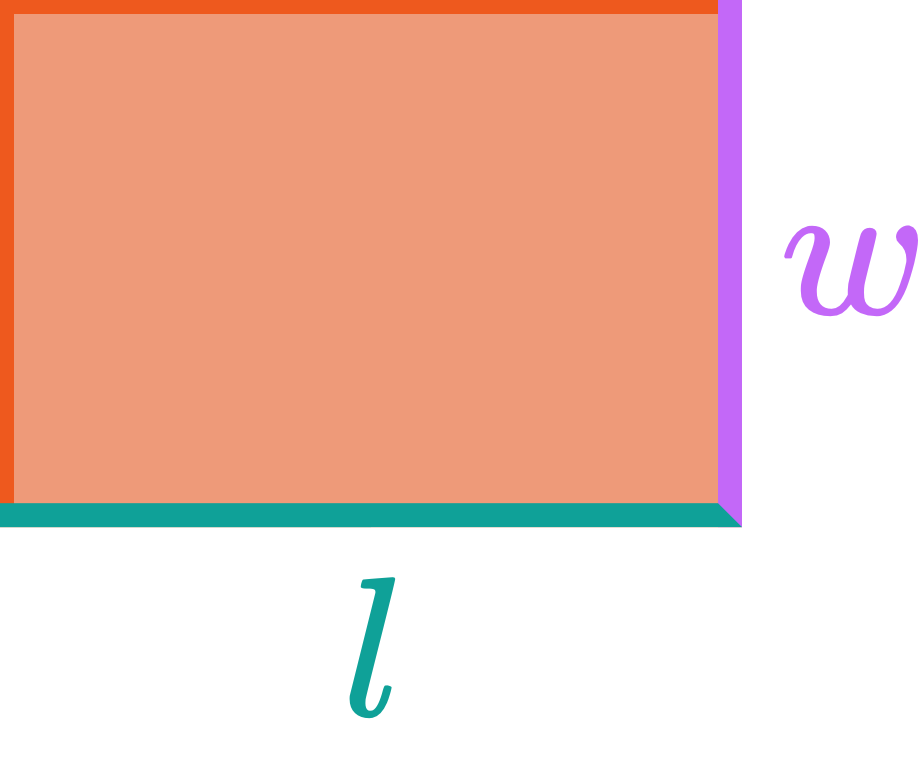
Step 2. Multiply the length by the width.

So, our answer is .
We have some questions for you! Help us out through this
INTRO
—
When we’re asked to find the area of a quadrilateral, what we’re really looking for is the amount of space inside the boundaries or sides that connect to make the shape.
Let’s imagine we want to build a small field in a Minecraft world and need to figure out the amount of land (area) in a 3 × 5 field.
We can start with a strip of land that has blocks of grass.
And then we just need to copy this row times.
Now, we have rows of grass blocks, giving us a total of blocks.
This is area 😮. By multiplying the length by the width, we get the amount of space inside the sides of a rectangle.
Multiplying a shape's length (or base) by its width (or height) is a pattern you’ll notice when solving for the area of different quadrilaterals:
ShapeImageFormula
Rectangle
Square
Parallelogram
Rhombus / Kite
Trapezoid
Check out our
Calculator
or explore our
Lesson
and
Practice
sections to learn more about how to find the area of quadrilaterals and test your understanding.

You can also use the Quick Links menu on the left to jump to a section of your choice.

You can also use the Quick Links dropdown above to jump to a section of your choice.

KEY STEPS
—

How to Find the Area of a Quadrilateral

Shape:

Step 1. Identify the length & width of the rectangle.

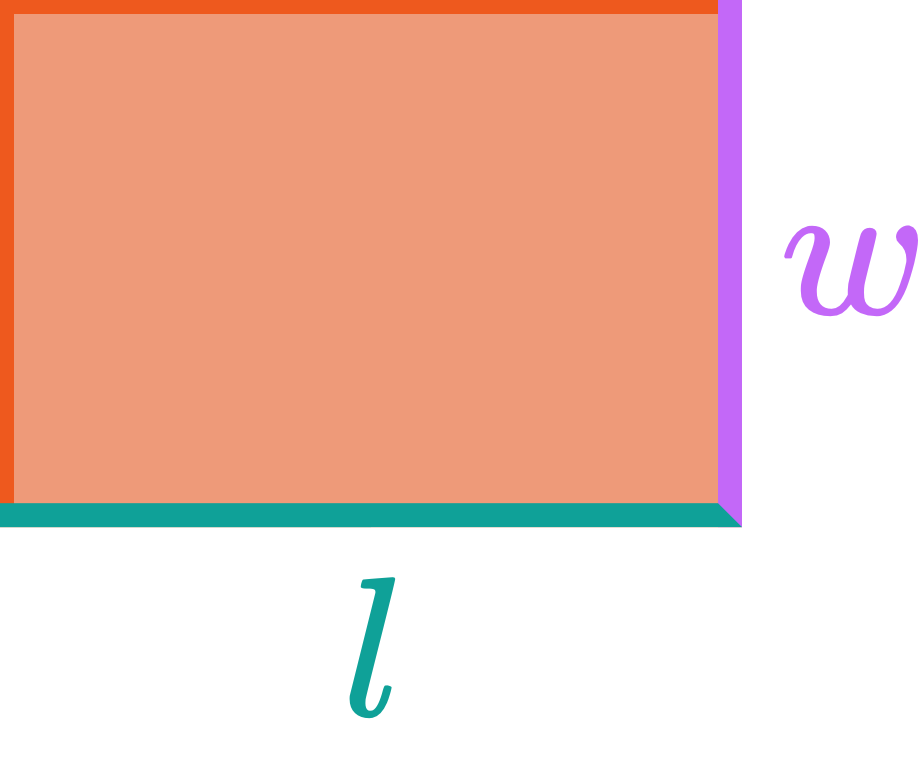
Step 2. Multiply the length by the width.

Step 1. Identify the side length of the square.

Step 2. Square the side length.

Remember, all the sides of a square are equal to each other, so .

Step 1. Identify the base and height of the parallelogram.

Step 2. Multiply the base by the height.

Remember, a parallelogram can be rearranged to form a rectangle.

Step 1. Identify diagonal/cross lengths of the rhombus.

Step 2. Multiply the diagonal/cross lengths.

Step 3. Divide by .

Remember, a rhombus can be rearranged to make a parallelogram.

Step 1. Identify the base lengths and height of the trapezoid.

Step 2. Add the base lengths.

Step 3. Multiply the sum of the base lengths by the height.

Step 4. Divide by .

Remember, two trapezoids can be rearranged to make a parallelogram.
LESSON
— Area of Rectangles & Squares
PRACTICE
— Area of Rectangles & Squares
LESSON
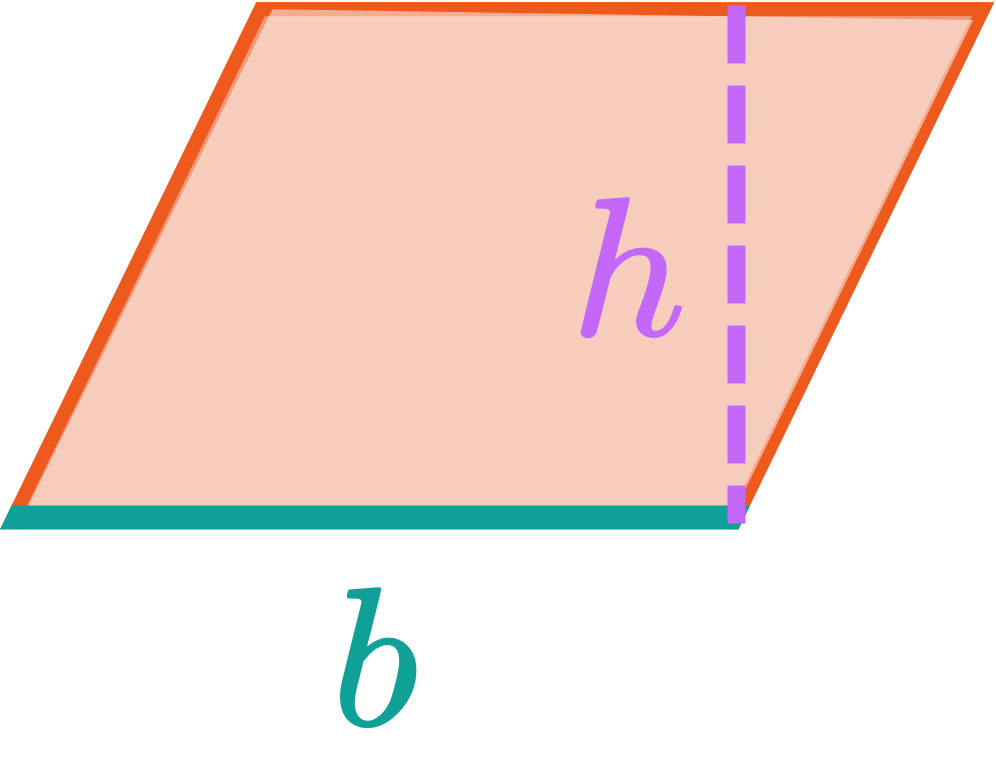
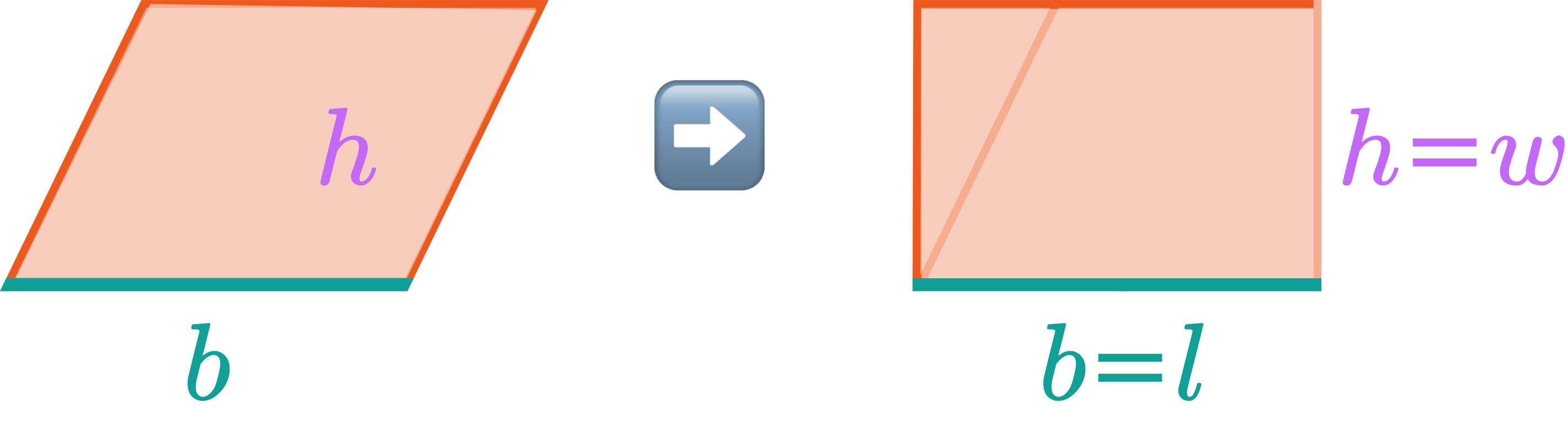
— Area of Parallelograms
PRACTICE
— Area of Parallelograms
LESSON
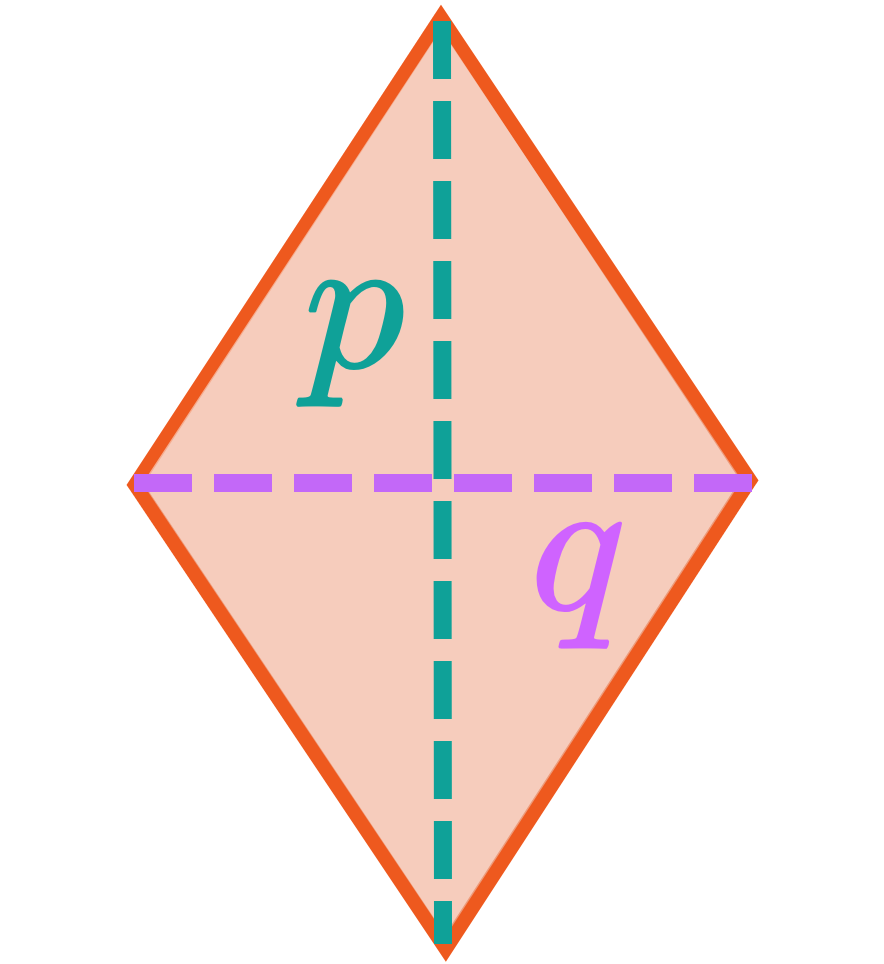
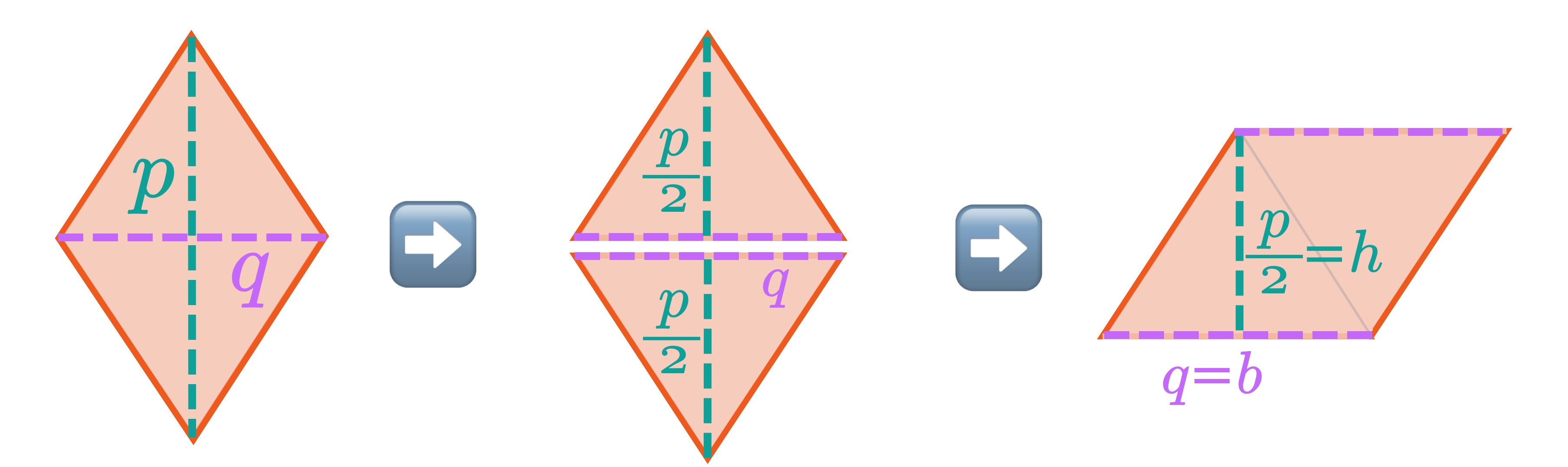
— Area of Rhombuses & Kites
PRACTICE
— Area of Rhombuses & Kites
LESSON
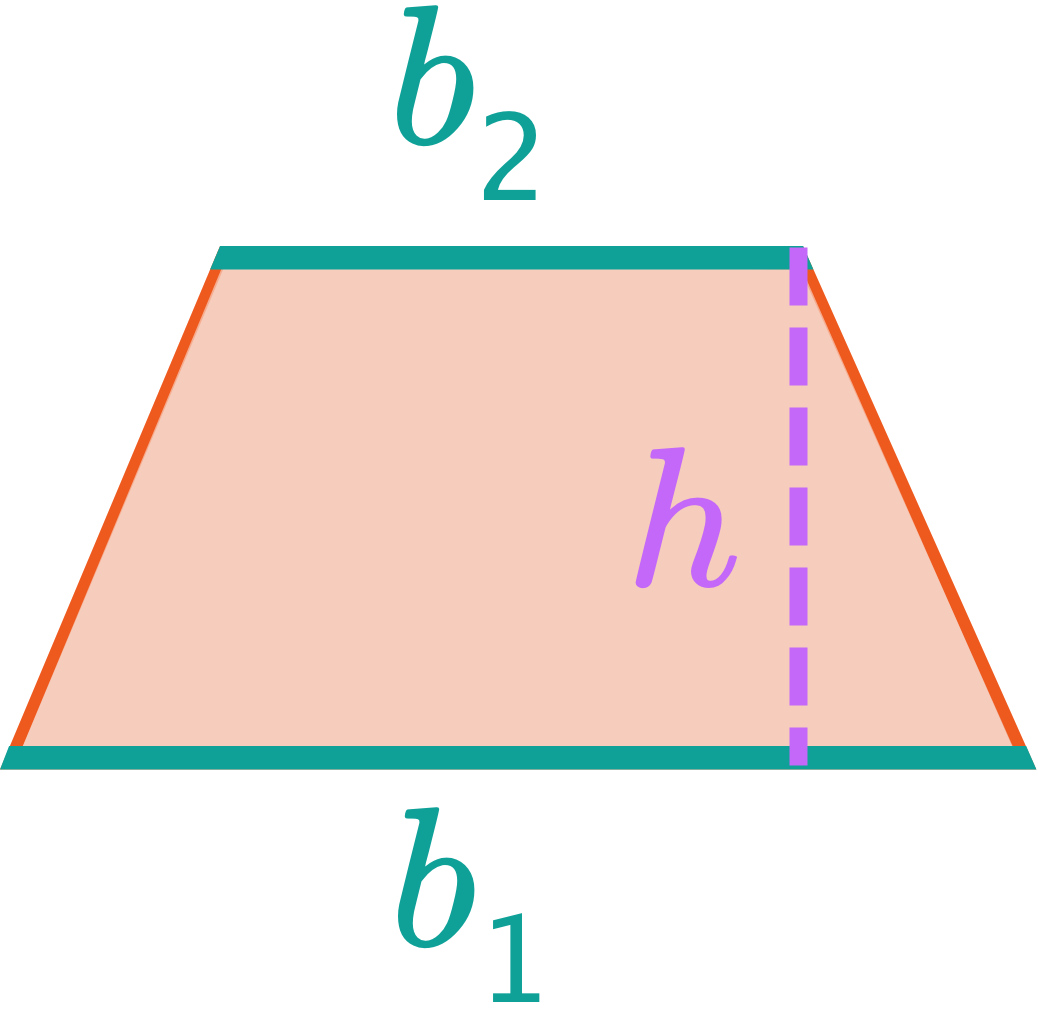
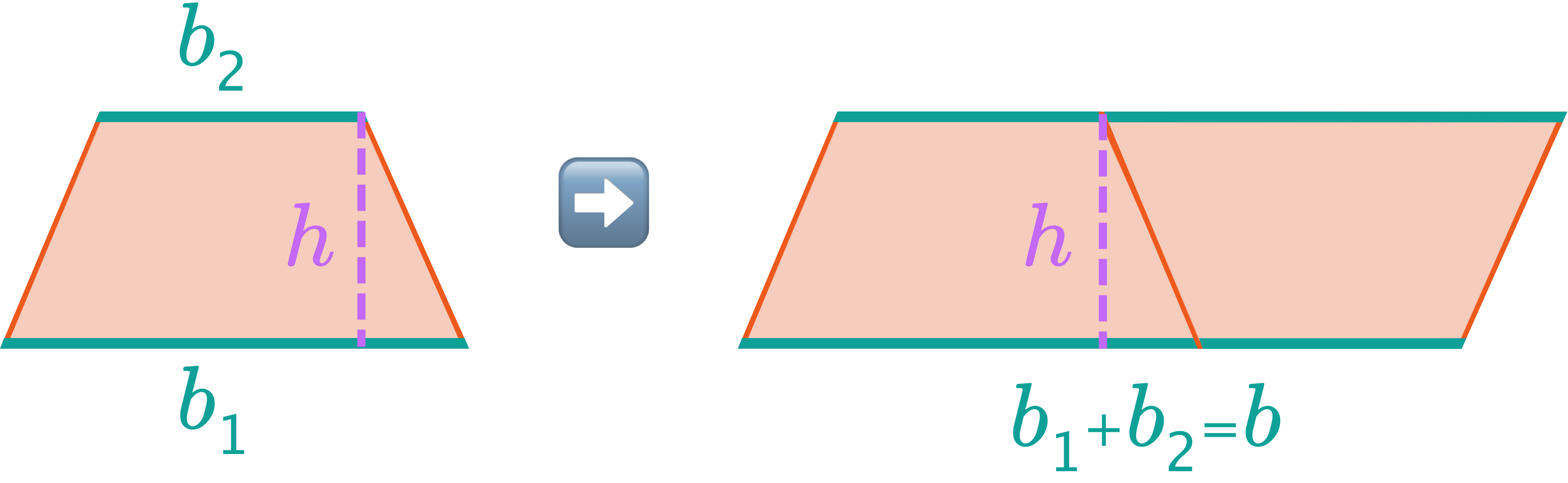
— Area of Trapezoids
PRACTICE
— Area of Trapezoids
CONCLUSION
—
Leave Feedback