QUICK LINKS

STUDENT
TEACHER

Area of Triangles Calculator

QUICK LINKS

STUDENT
TEACHER

Area of Triangles Calculator

Area of Triangles

CALCULATOR
—

Area of Triangles Calculator

What does your triangle look like?

Step 1. Identify the base and height of the triangle.

Imagine the triangle is a mountain. The base must be flat and the height connects the base of the mountain to the peak.

Step 2. Multiply the base by the height.

Step 3. Divide by 2.

So, the area of the triangle is .
We have some questions for you! Help us out through this
INTRO
—
When we’re asked to find the area of a triangle, what we’re looking for is the amount of space inside the sides of our triangle.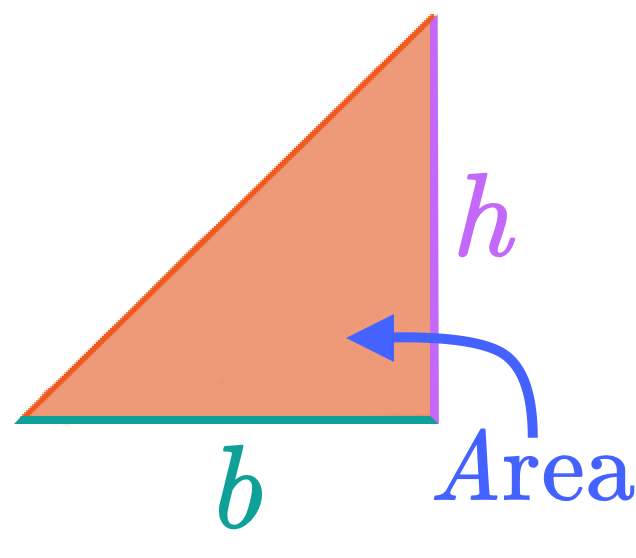
The formula is pretty straightforward, but correctly identifying the base and the height of the triangle can sometimes be tricky. That’s why we like to imagine triangles as mountains!

Type of Triangle:

We can imagine the triangle as a mountain where the base is flat (⬌), and the height is a vertical line that connects the base to the peak (⬍).
Sometimes, we may need to rotate our triangle in order for it look like a mountain:Check out our
Calculator
or explore our
Lesson
and
Practice
sections to learn more about how to find the area of triangles and test your understanding.

You can also use the Quick Links menu on the left to jump to a section of your choice.

You can also use the Quick Links dropdown above to jump to a section of your choice.

KEY STEPS
—

How to Find the Area of a Triangle

Step 1. Identify the base and height of the triangle.

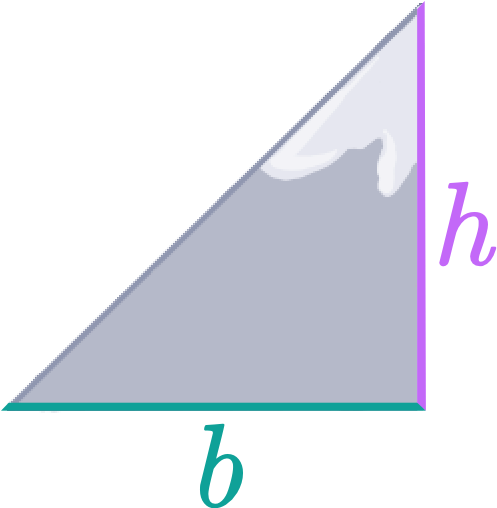
Imagine the triangle is a mountain. The base must be flat and the height connects the base of the mountain to the peak.

Step 2. Multiply the base by the height.

Step 3. Divide by 2.

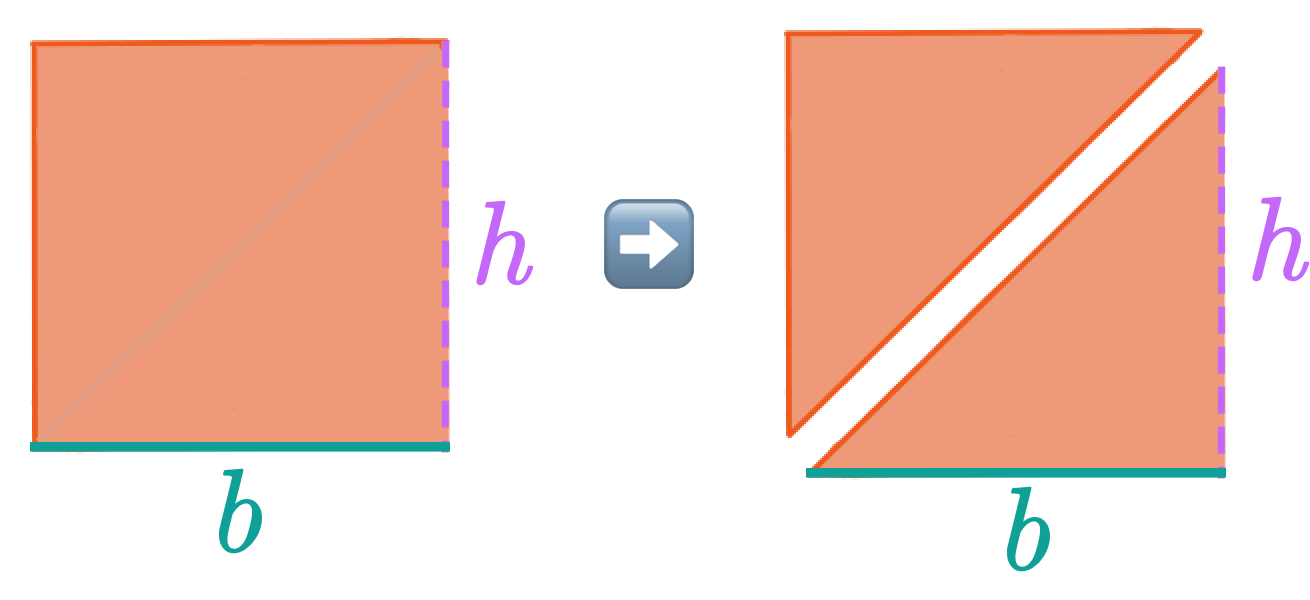
We divide by 2 because the area of a right triangle is equal to ½ the area of a rectanglemade up of two right triangles with the same base and height.
LESSON
— Right Triangles
PRACTICE
— Right Triangles
LESSON
— Acute Triangles
PRACTICE
— Acute Triangles
LESSON
— Obtuse Triangles
PRACTICE
— Obtuse Triangles
CONCLUSION
—
Leave Feedback