CALCULATOR
—
Circumference & Area of Circles Calculator
Step 1. Identify the unknown.
What are you trying to solve for?
We have some questions for you! Help us out through this
INTRO
—
Remembering all the different parts of a circle and what they represent can sometimes feel a little out of reach. That’s why we like to think about them in terms of our favorite type of circle...pizza!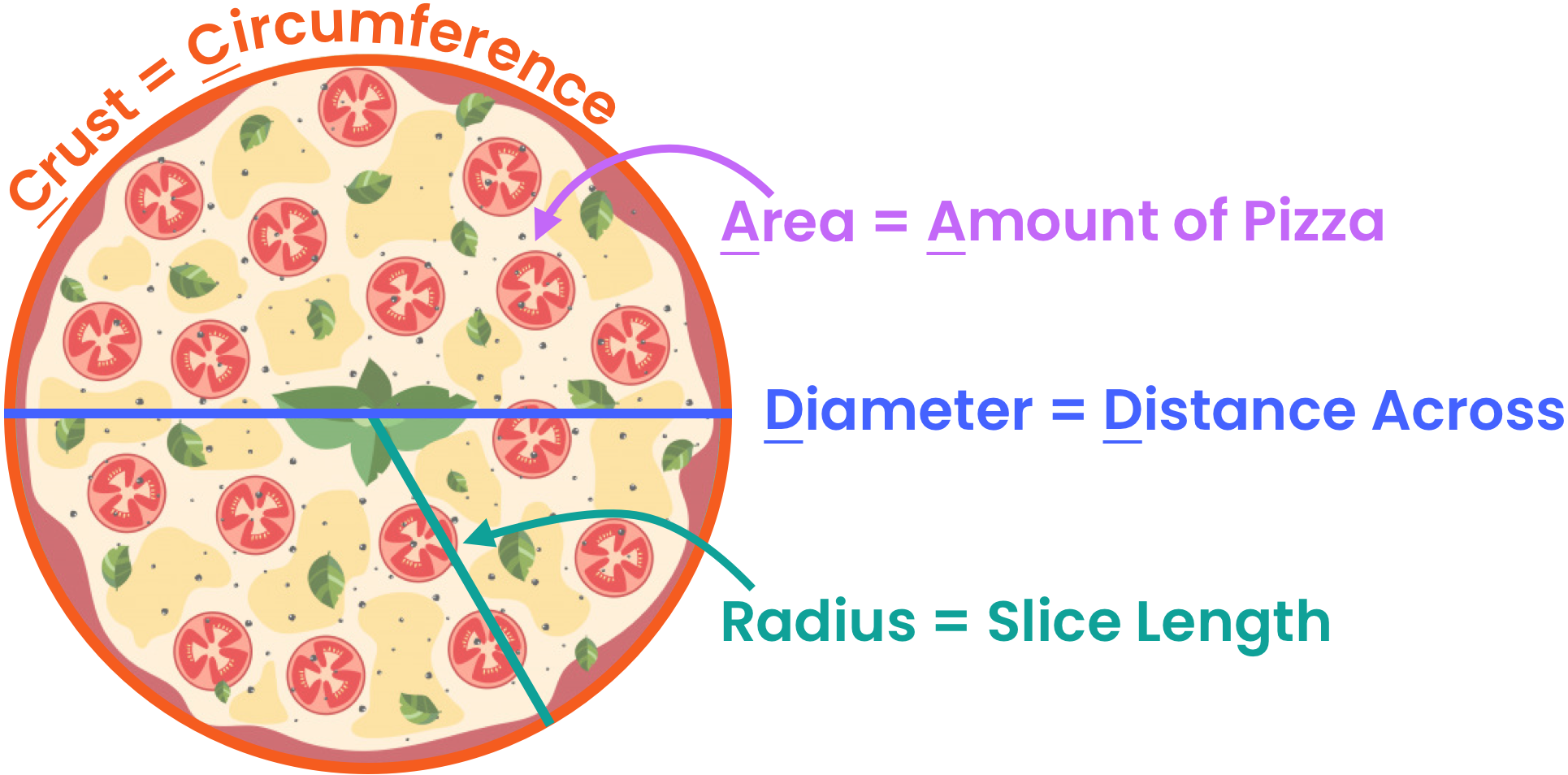
These are different formulas we can use to find these different values:
Check out our | Circle Part | Pizza | Formula |
| Circumference | Crust | |
| Area | Amount of Pizza | |
| Diameter | Distance Across | |
| Radius | Slice Length |
Calculator
Lesson
Practice
You can also use the Quick Links menu on the left to jump to a section of your choice.
You can also use the Quick Links dropdown above to jump to a section of your choice.
KEY STEPS
—
How to Find Circumference & Area of Circles
Step 1. Identify the unknown.
What are you trying to solve for?
Since the unknown is the circumference, you need to solve for the distance around the circle, which is like the crust of a pizza.
Step 2. Identify the given.
What information do you already have?
Step 3. Select the correct formula(s).
You can use the following formula(s) to solve for the circumference the given the radius:
Step 4. Plug in the given and solve for the unknown.
Plug in the given value into the formula and solve for the unknown using inverse operations as needed.
LESSON
— Diameter Formula
PRACTICE
— Diameter Formula
LESSON
— Circumference Formula
PRACTICE
— Circumference Formula
LESSON
— Area Formula
PRACTICE
— Area Formula
CONCLUSION
—
Leave Feedback