CALCULATOR
—
Function Calculator
We have some questions for you! Help us out through this
INTRO
—
A function defines the relationship between an input and an output.
In order for the relationship to be considered a function, each input can only have one output. However, multiple inputs can have the same output.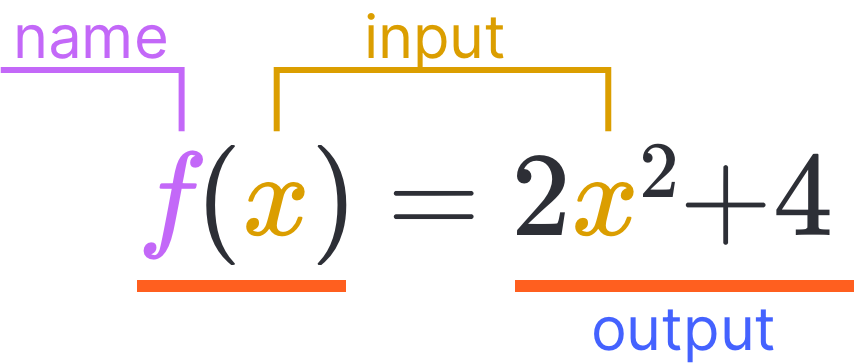
The function, named , takes some number as an input, squares it, multiplies by 2, and then adds 4 to produce its output.Check out our or explore our and sections to learn more about functions and test your understanding.
Functions operate a lot like vending machines. When we enter a code into a vending machine, we get a specific drink. When we enter an input into a function, we get an output. Try it out!
Function Vending Machine (drinks)
A1
A2
A3
B1
B2
B3
C1
A
B
C
1
2
3
In our vending machine above, this is like how each code gets us one specific drink (B1 always gives us water), but there can be multiple codes that can get us the same drink (to get water, we can input B1, B2, or B3).
Parts of a Function
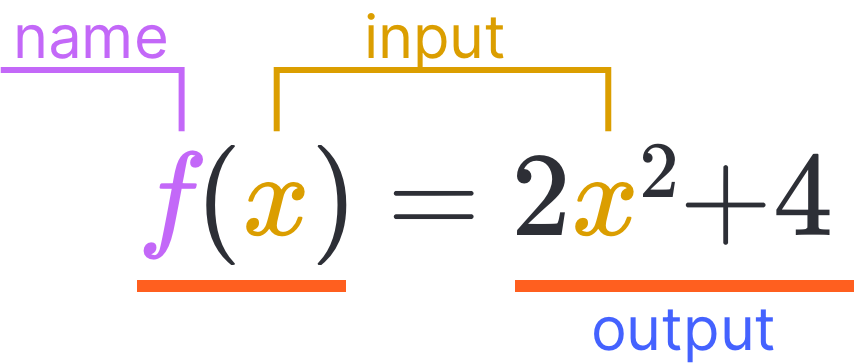The function, named , takes some number as an input, squares it, multiplies by 2, and then adds 4 to produce its output. Calculator
Lesson
Practice
You can also use the Quick Links menu on the left to jump to a section of your choice.
You can also use the Quick Links dropdown above to jump to a section of your choice.
KEY STEPS
—
How to Evaluate a Function
Step 1. Plug in the input.
Plug in the input wherever the variable shows up in the function.
Imagine this as entering the code for a drink we want from a vending machine.
Step 2. Calculate the output.
Use order of operations (PEMDAS) to calculate the output.
Imagine this as the vending machine processing the code to dispense the drink.
LESSON
— Evaluating Functions
PRACTICE
— Evaluating Functions
CONCLUSION
—
Leave Feedback