CALCULATOR
—
Surface Area of Cylinders Calculator
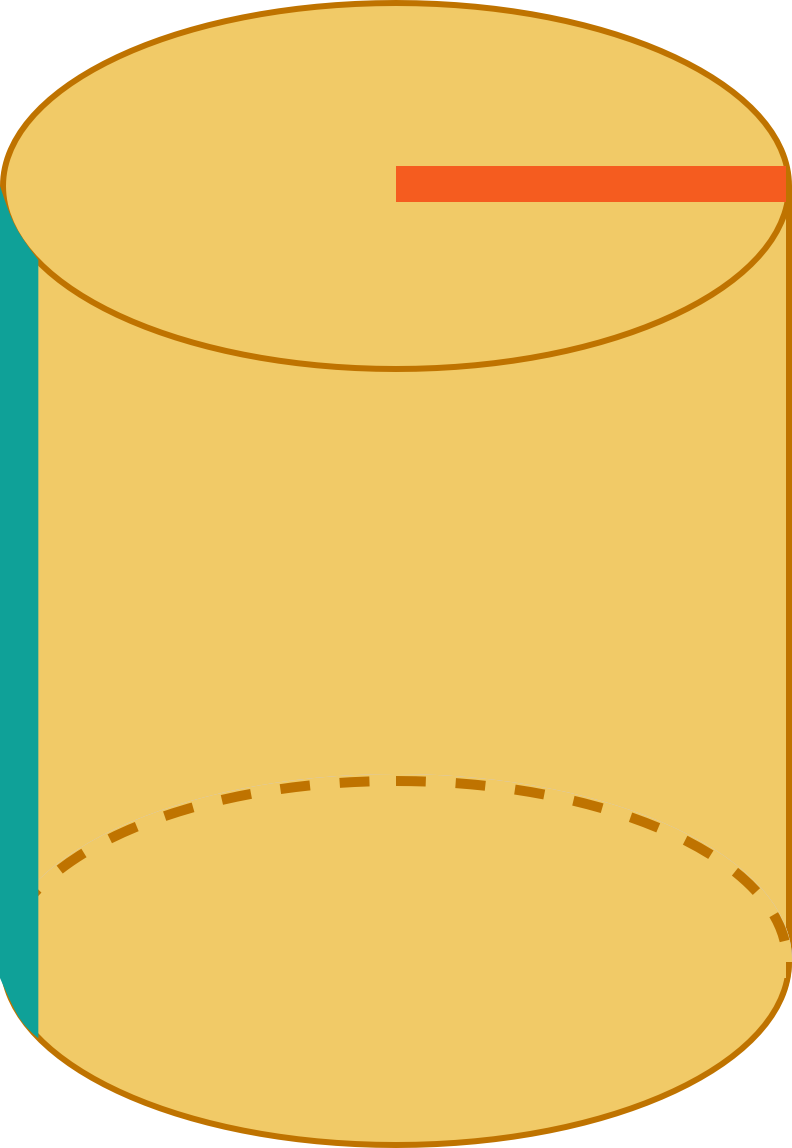
We have some questions for you! Help us out through this
INTRO
—
The surface area of a 3D shape is equal to the sum of the areas of all the faces (sides) of that shape. A helpful way to think about it is:
If we were to unwrap a gift, the amount of wrapping would be equal to the surface area of the object it was covering.
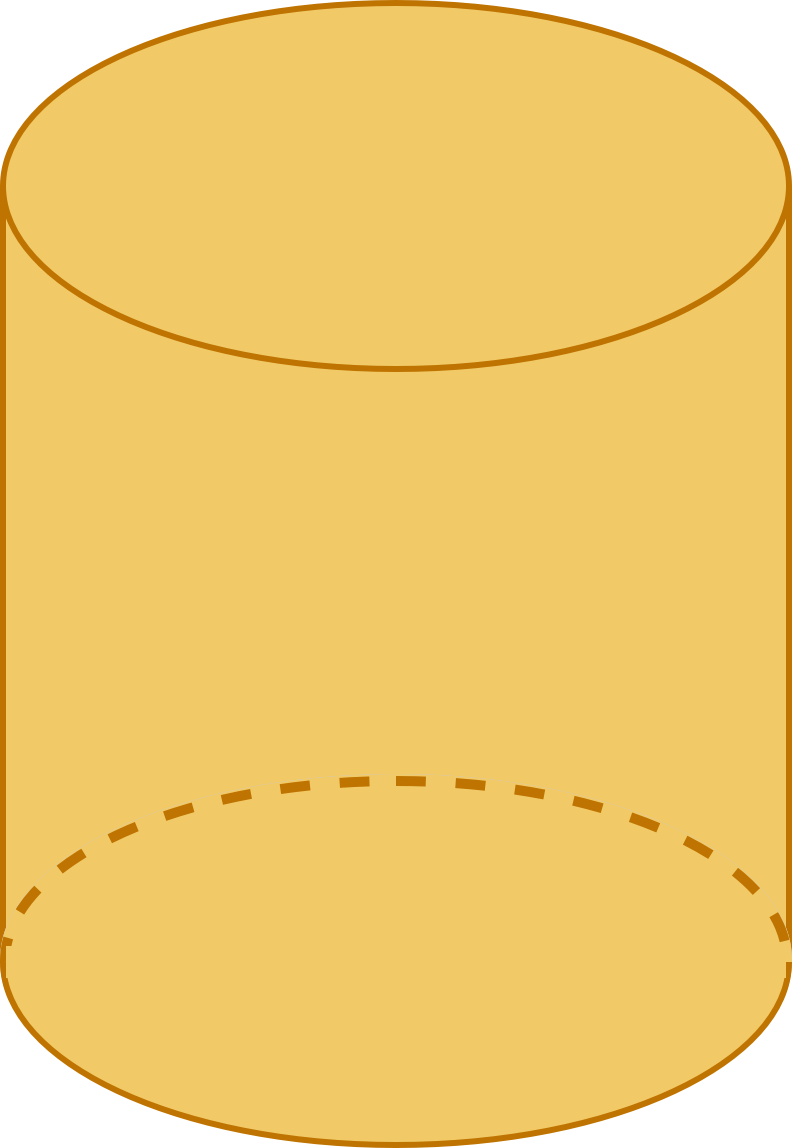
When we “unwrap” a 3D shape, we get what we call a net. A surface area net shows us the different 2D shapes that make up the faces of the 3D shape.When working with pyramids, cylinders, and cones, you may also be asked to find the lateral surface area.Check out our or explore our and sections to learn more about how to find the surface area of cylinders and test your understanding.
surface area = sum of face areas
We can also think about surface area in terms of gifts! The surface area is like the minimum amount of wrapping paper we need to prep a gift for its surprise reveal. 🤩If we were to unwrap a gift, the amount of wrapping would be equal to the surface area of the object it was covering.We can then find the area of each face and then add them all together to find the total surface area.
What is lateral surface area?
Lateral surface area is simply the total surface area of an object minus the area of its base(s).
Calculator
Lesson
Practice
You can also use the Quick Links menu on the left to jump to a section of your choice.
You can also use the Quick Links dropdown above to jump to a section of your choice.
KEY STEPS
—
How to Find Surface Area of Cylinders
Step 1. Unwrap the cylinder.
Step 2. Calculate the area of each part of the net that makes up the cylinder.
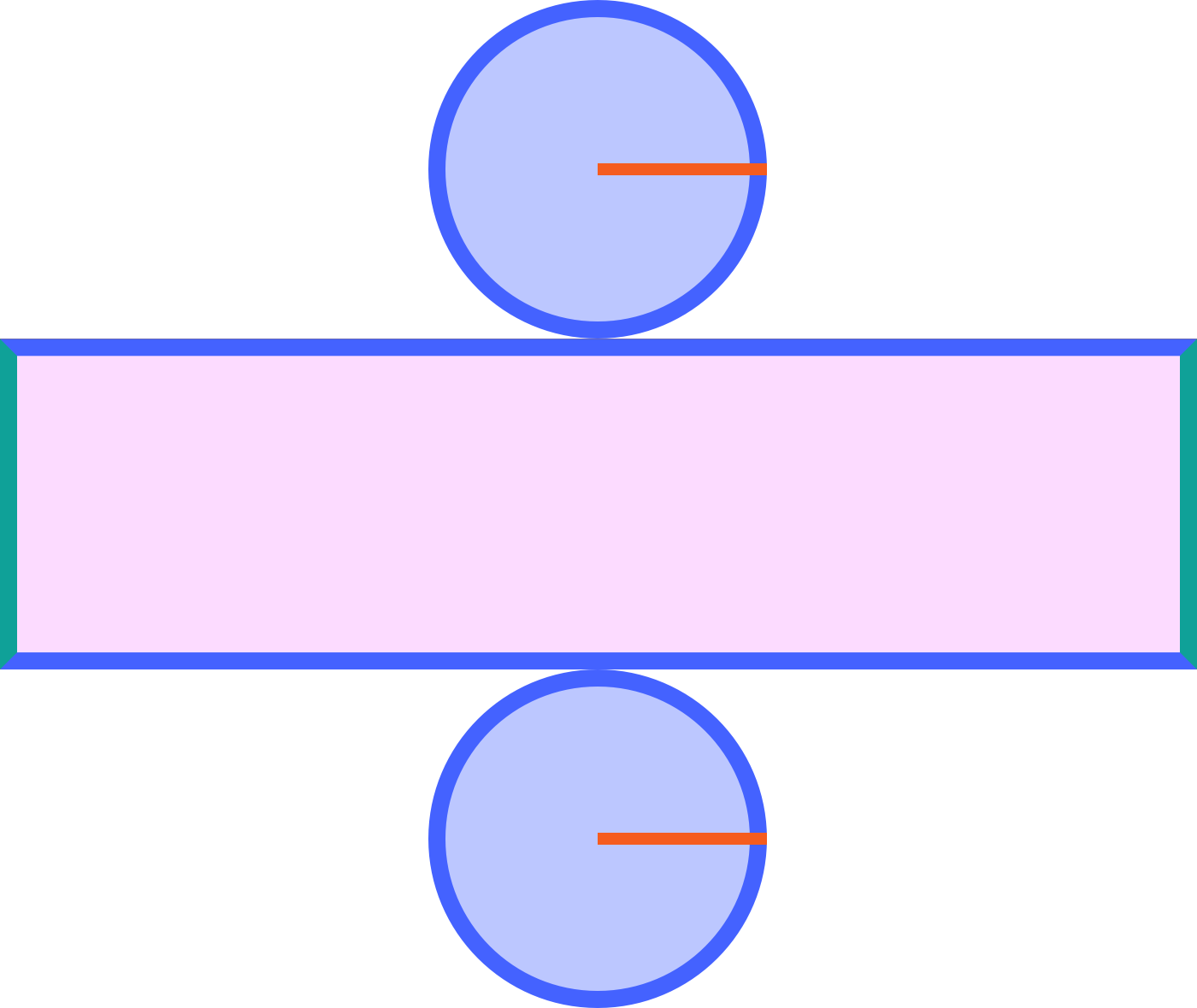
| Rectangle | |
| Circles |
Step 3. Add up the areas of the shapes that make up the cylinder.
LESSON
— Surface Area of Cylinders
PRACTICE
— Surface Area of Cylinders
CONCLUSION
—
Leave Feedback