QUICK LINKS

STUDENT

TEACHER

Volume of Cylinders and Prisms Calculator

Was this lesson helpful?

Why wasn't it helpful?

Which sections were not helpful?

Anything else?

STUDENT TEACHER

QUICK LINKS

STUDENT

TEACHER

Volume of Cylinders and Prisms Calculator

Volume of Cylinders and Prisms

CALCULATOR

—

Volume of Cylinders & Prisms Calculator

What is your shape?

Step 1. Imagine & identify the base.

We can think of the cylinder as a cake with layers shaped as circles. The base is the bottom layer, a circle.

r

r

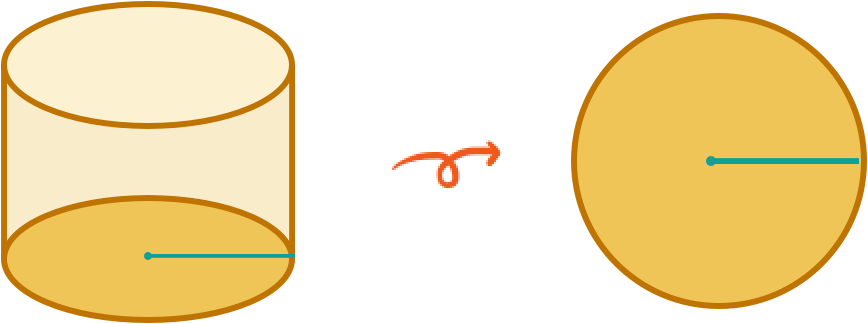
We have some questions for you! Help us out through this

survey

INTRO

—

Volume tells us the amount of space there is inside a 3D shape. It’s kind of like the 3D version of area 🤯. To find the volume of a cylinder or prism, we multiply the area of the base by the height.

V olume = base area \times H eight

To help us understand why this is the formula for volume, let’s imagine we have a cake with lots of layers.

Shape	Volume
Cylinder $H$ $u n d e f i n e d$ $u n d e f i n e d$ $u n d e f i n e d$ $u n d e f i n e d$ $r$	$V = π r^{2} \times H$
Rectangular Prism $H$ $l$ $w$ $u n d e f i n e d$ $w$ $u n d e f i n e d$	$V = l w \times H$
Triangular Prism $H$ $u n d e f i n e d$ $h$ $b$ $h$ $u n d e f i n e d$	$V = \frac{1}{2} b h \times H$

KEY STEPS

—

How to Find the Volume of Cylinders & Prisms

Shape:

Step 1. Imagine & identify the base.

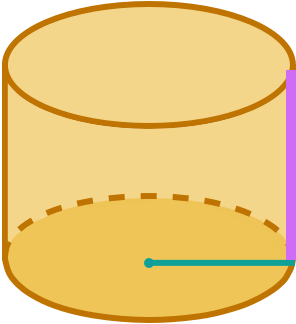
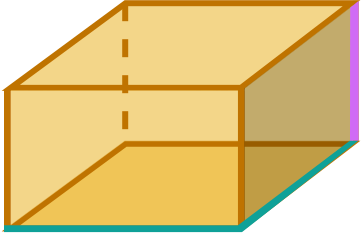
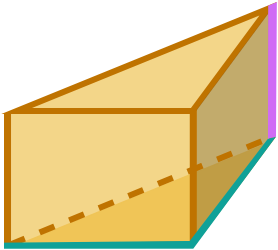
We can think of the cylinder as a cake with layers shaped as circles. The base is the bottom layer, a circle.

Step 2. Calculate the area of the base.

We start by calculating the area of the base circle.

V = (π r^{2}) \times H

Step 3. Multiply the area of the base by the height (H) of the cylinder.

Then, we multiply the base area by the height to get the volume.

V = (π r^{2}) \times H

LESSON

— Volume of Cylinders & Prisms

PRACTICE

— Volume of Cylinders & Prisms

CONCLUSION

—

Leave Feedback

Math Lessons

For Teachers

Other Resources
SAT Prep
Blog

About

Support Us
Merch
Donate

Help

Log In

QUICK LINKS

QUICK LINKS

Volume of Cylinders and Prisms

Volume of Cylinders & Prisms Calculator

Step 1. Imagine & identify the base.

Step 2. Calculate the area of the base.

Step 3. Multiply the area of the base by the height (H) of the cylinder.

How to Find the Volume of Cylinders & Prisms

Step 1. Imagine & identify the base.

Step 2. Calculate the area of the base.

Step 3. Multiply the area of the base by the height (H) of the cylinder.